流动性树，DeFi的未来？

一键发币： SUI | SOL | BNB | ETH | BASE | ARB | OP | POLYGON | AVAX | FTM | OK

在本文中，我们将讨论一种新的 DeFi 原语，我们将其定义为流动性树（liquidity tree）。这些原语是 SYS Labs 支持的即将发布的 Pachira 代币的核心功能。

自从这个主题首次概念化（即 2023 年 6 月）以来，我一直在热切地等待大约一年的时间来撰写有关它的文章。在此之前，我和 cyotee（即流动性树的共同发明者和 OympusDAO 的前首席开发人员）花了大约一年半的时间进行了大量探索性工作（即自 2022 年初以来）。所以总的来说，这已经进行了近 2.5 年的研究和开发。

在我的 ETHDenver 2024 演讲中，这可以被认为是我们首次正式公开亮相这个原语，我宣称流动性树将定义 DeFi 进化的下一个时代。我注意到社区中的其他几个人从谈话中选出了这句话，并在各种推文和在线讨论中使用它。我发现这有点有趣，因为当我感知到这个想法时，我就是这么看待它的。

因此，作为我关于流动性树原语的第一篇介绍性文章，我认为这将是一种有趣的方式来深入了解这个令人兴奋的新概念。SYS Labs 团队的其他成员告诫我要保持这篇文章的高水平，因此这将是记录这一内容的第一步。

1、自动做市商的演变

DeFi 的故事真正开始于 Vitalik Buterin（即以太坊创始人）在 2016 年的 Reddit 帖子，他在帖子中提出了自动做市商 (AMM) 的原始想法。一年后，Hayden Adams 开始致力于将这个想法变成一个功能性产品，并创立了 Uniswap。

1.1 第一代 AMM：恒定乘积做市商

AMM 协议是去中心化交易所 (DEX) 使用的机制，最早由 Uniswap 引入，Uniswap 于 2018 年 11 月在以太坊主网上推出。

这些 DEX 由各种交易对（例如 ETH/USDC、ETH/WBTC 等）代表的流动性池 (LP) 组成，充当 AMM。这些 LP 中的交易活动通过智能合约通过恒定乘积交易 (CPT) 公式（即 xy = k）进行管理。

1.2 第一代 AMM：恒定均值做市商

2019 年 9 月，Balancer Labs 发布了白皮书，详细介绍了 2020 年 3 月推出的恒定均值做市商。这可以有效地看作是恒定乘积做市商理念的延伸，包括具有任意权重的 N 种资产的流动性池（即 (x0x1 … *xN)^(1/N)=k ）。

1.3 第二代 AMM：混合 CPMM

第一波创新带来了滑点、无常损失和资本效率等问题。因此，随着 2020 年加密货币夏季的到来，新一代 AMM 的诞生，Curve 的 Stableswap 也应运而生。正是在这里，他们有了将恒定均值做市商 (CMMM) 和恒定和做市商 (CSMM) 结合到混合 CPMM 中的洞察力。

CSMM 具有在交易过程中产生很少滑点的特性，而 CMMM 则确保市场有足够的深度来促进交易。因此，Stableswap 的解决方案最适合稳定代币（例如 USDC、USDT）的交易，因为它提供了一种高效的机制来缓解滑点，同时确保高效的流动性供应。

1.4 第二代 AMM：虚拟自动做市商

受 Uniswap 等第一代 AMM 的启发，结合使用 Synthetix 创建合成资产的想法，Perpetual Protocol 于 2020 年 12 月发布了虚拟自动做市商 (vAMM)。vAMM 不是交换实际资产，而是用于交换衍生品合约等虚拟资产。

通过利用虚拟资产，vAMM 比第一代 AMM 提供更高的资本效率和更好的定价。

1.5 第二代 AMM：鲜为人知的原语

还有其他值得一提的第二代 AMM，它们都解决了无常损失和资本效率问题。 Bancor 引入了自动代币交易和单边质押。Sushiswap 引入了流动性挖矿的概念。

在此期间，我们还出现了 1Inch、Paraswap 和 OpenOcean 等 DEX 聚合器。

1.6 第三代 AMM：集中流动性做市商

2021 年 5 月，Uniswap 推出了 V3 作为升级版，以解决懒惰流动性问题，从而引入了集中流动性做市商 (CLMM) 协议。此次升级背后的主要思想是将流动性集中在活跃交易区间内，这实际上加深了订单簿，使更多的流动性可用于交易；

有关更多详细信息，请参见图 1。该协议可以说是第一个通过 AMM 流动性频率分布来解决市场效率问题的协议。

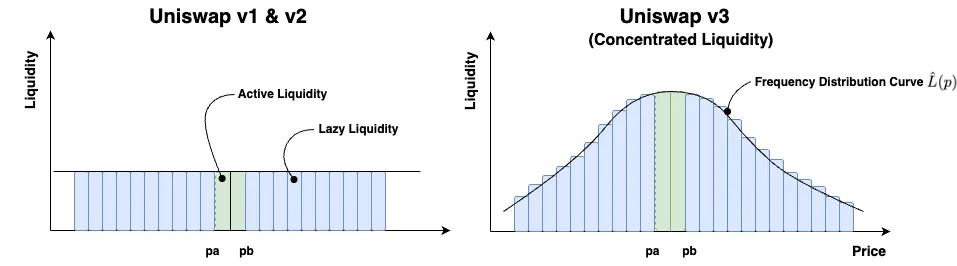
在我们的 ETHDenver 演讲中，我们开始讨论 Uniswap V2 中处于活跃交易范围之外的非活跃资本（称为惰性流动性）如何无法获得收益。这就是所谓的资本效率低下。

Uniswap V3 通过调整流动性频率分布来解决此问题，将流动性集中在其活跃交易区域（Pa，Pb）周围，如图 1 所示。通过这样做，流动性池（LP）内的订单簿实际上得到了加深，从而提供了更多资本来进行更大的交易。

图 2 中的价格曲线说明了这一点。根据 Uniswap 的说法，相对于 Uniswap V2，这种设计增强可以提供高达 4000 倍的资本效率。

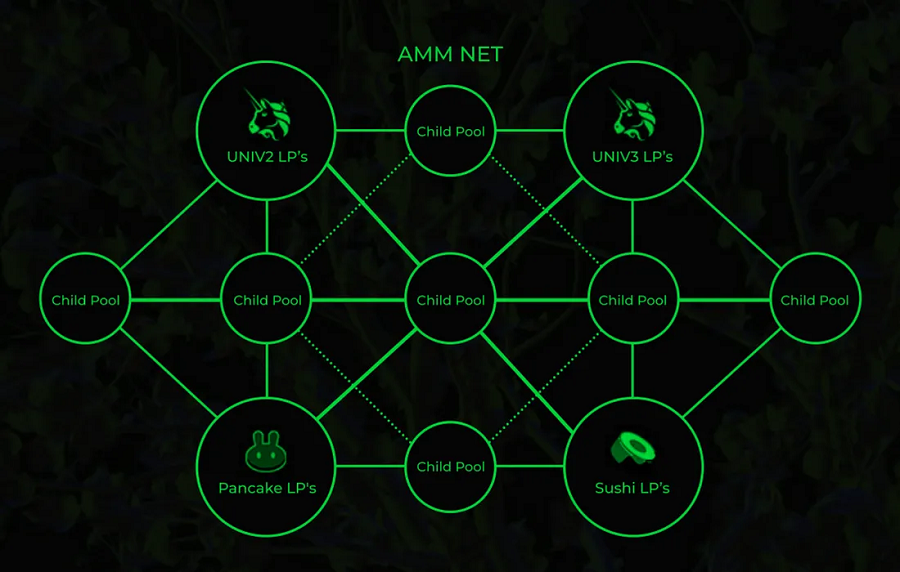
2、使用流动性树联网 AMM

在上一节中，我们简要概述了 AMM 协议的演变。上述所有协议的统一特征是它们都是单一的 AMM 协议。在本节中，我们将讨论 AMM 网络，简称 AMM 网络。

当 AMM 网络被纳入合约代码时，它打开了一个充满机会的潘多拉盒子，因为上一节中提到的所有协议都可以配置成 AMM 网络。流动性树可以被认为是最简单的 AMM 网络类，我们将在本次讨论中重点介绍这种网络的优势。

如果我们重新审视图 1 中的集中流动性分布，我们想要解决的问题是如何在活跃交易区间之外使用资本，以便同时获得回报

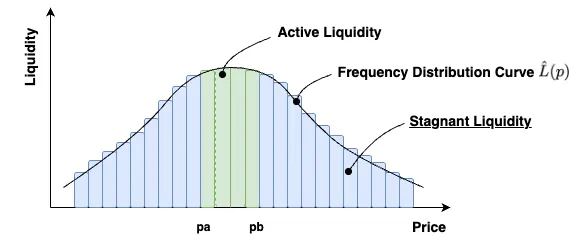
如果我们参考图 3，我们解决的是将活跃交易带之外的剩余流动性视为停滞流动性问题的问题。与使用单个 LP 解决这个问题不同，正如 AMM 的整个演变过程中所引用的那样，我们使用 LP 网络（称为流动性树）来解决这个问题。

2.1 让我们包含一个新的维度（对于理解至关重要）

我听很多degen人士说过，掌握这个概念可能很难。然而，我恳请你不要略过这个关键步骤，并花点时间思考我们在这里做什么。

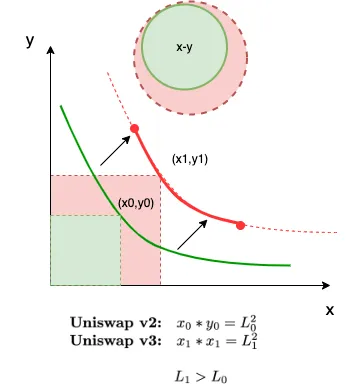
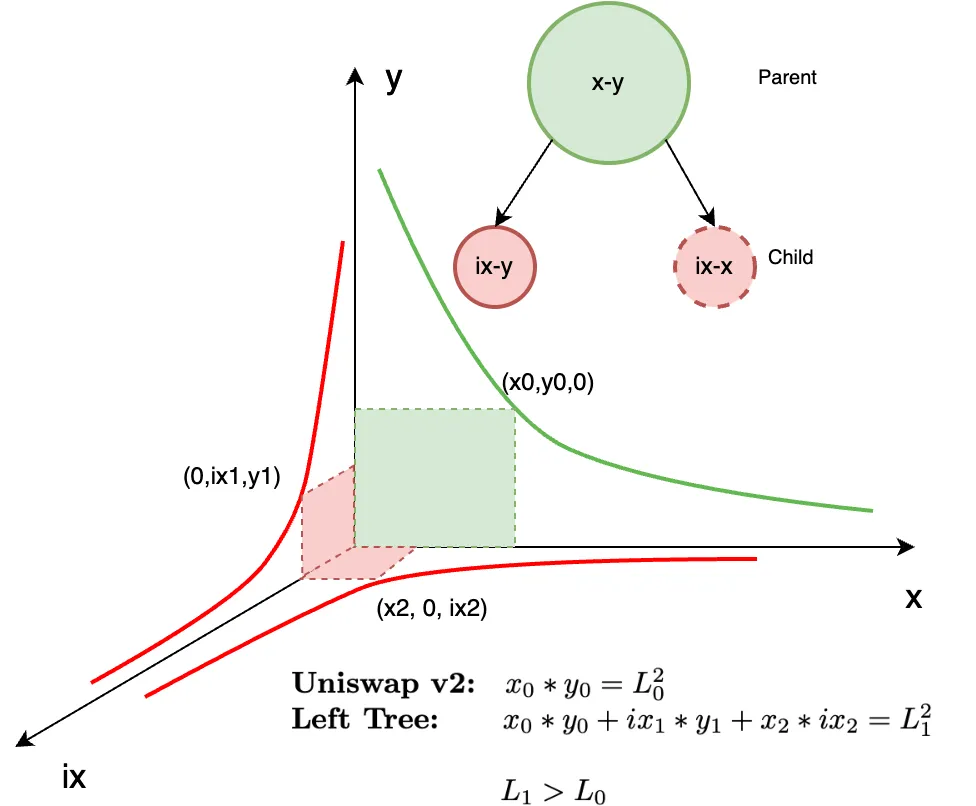
如果你能从概念上理解这部分，以及（更重要的是）我们为什么要这样做，那么将解决方案扩展为更一般的表示只是一步一步重复。所以让我们以图 2 所示的常见 CPT xy 价格曲线为例，并通过包含一个新维度进行扩展，如图 4 所示。

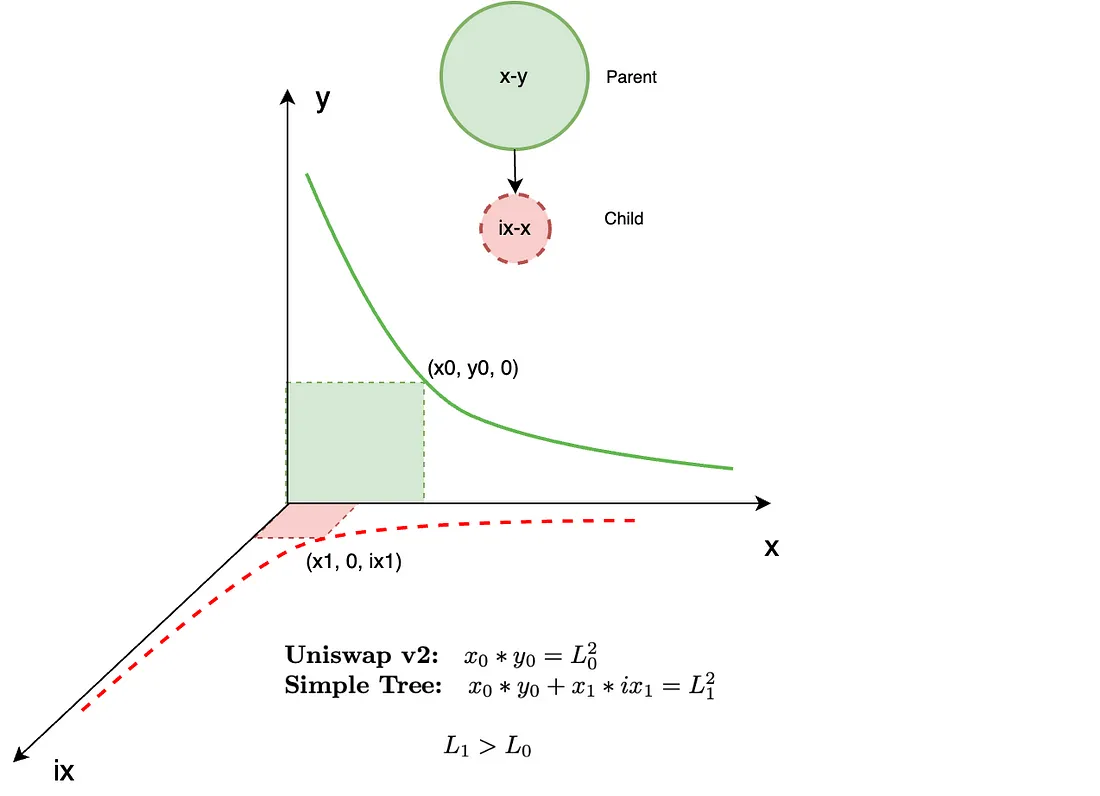
与标准 CPT 公式不同，我们现在考虑的是 x、y 和索引 x（也称为 ix），而不是 x 和 y。当我们说索引时，我们使用经济定义，即将经济数据编译成单一指标或测量值。在流动性树的情况下，我们的经济数据是 LP 代币的数量，以两种资产（x 或 y）中的任一种来衡量，如图 5 所示。

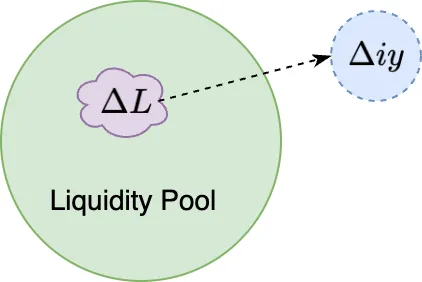
例如，假设我们有一个 USDC/ETH LP 并从该池中取出 10 个 LP 代币。我们以定义为 iUSDC 或 iETH 的指数代币的形式，以 USDC 或 ETH 为索引，为这 10 个 LP 代币。因此，随着 USDC/ETH 价格的变化，iUSDC 或 iETH 的数量也会发生变化！

解决 CPT 索引问题通常涉及求解线性方程组，你可以在我之前的一篇文章中阅读有关该问题的更多信息，标题为：Uniswap 索引问题。去年我们发布这篇文章的时候，社区里几乎没有人对此发表评论，因为直到现在我们才揭示其背后的重要性。如果不先定义和解决这个问题，我们就无法实现流动性树。

让我们回顾一下；要创建流动性树，我们需要从其池中获取两个 LP 资产（例如 x 和 y）和一定数量的 LP 代币，并将它们索引到 ix 和/或 iy 中。这些索引代币源自我们的 LP 代币，这些代币不断重新调整为 x 和/或 y 的数量，这称为持续重新调整索引代币（CRIT）。这些 CRIT 被放回市场以形成子 LP，并与来自我们父 LP 的原始资产 x 或 y 之一配对；例如，参见图 4。

图 4 描绘了流动性树的最基本形式，称为简单树，由一个父 LP 和一个子 LP 组成。如果我们将 x 索引为 ix 并与 x 配对，我们可以将其表示为父 LP 在 x-y 平面上的曲线和子 LP 在 ix-x 平面上的曲线。同样，我们也可以将其表示为计算树，其中节点表示 LP 操作，节点之间的弧表示从父 LP 转移到子 LP 的索引流动性。

2.2 为什么要包括这些新维度？

我们为什么要包括这些新维度的简短答案是为了从我们的投资中获得更高的收益。当我们投资 LP 时，我们会收到 LP 代币，并期望通过收取随时间累积的交易费用份额来从该投资中获得回报。

有了流动性树，我们现在可以选择从我们投资的 LP 代币中铸造指数代币并将其重新投资到子 LP 中。通过这种方法，我们的投资现在既能从母 LP 获得回报，也能从子 LP 获得回报，从而产生更高的收益。我们实际上是在投资 LP，从该投资中获得全额抵押贷款并将其再投资。因此，我们既能从原始投资中获得收益，也能从全额抵押贷款中获得收益。

有关此想法背后的直觉，请参见图 6。

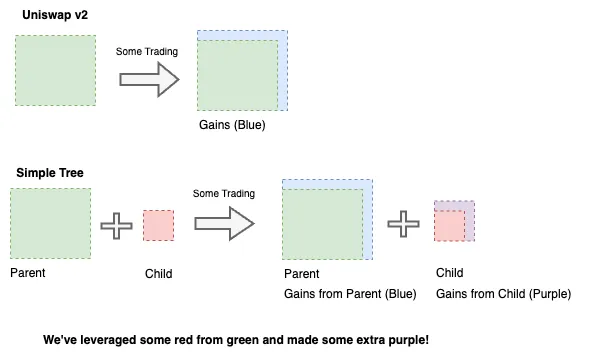
有些人可能会想，DeFi 社区不是通过 DeFi 收益耕作来做到这一点的吗？从某种意义上说，是的，但从技术上讲不是。对于经典的收益耕作，LP 代币头寸由最终用户手动处理，并且必须持续监控。

然而，通过流动性树，我们已经将这一过程形式化，并通过采用 CRIT 将其纳入合约代码，这只有通过首先解决索引问题才能实现。因此，最终用户不需要手动管理头寸，这反过来又解放了流动性提供者去做更复杂的事情，也允许设计师构建更复杂的产品。

正如我们将在后面的文章中展示的那样，通过我们即将发布的 Pachira 代币，这打开了一个潘多拉盒子，里面有以前作为去中心化机构技术无法实现的 DeFi 产品。因此，引入新的新兴效应，有可能重塑现实世界的人类社会行为。

我们可以看到，通过使用流动性树，我们解决了图 3 中定义的流动性停滞问题。随着这一过程的正式化，我们提高了市场效率。简而言之，正如我们在 AMM 的演变中所概述的那样，我们不是使用单个 LP 来解决这个问题，而是使用称为流动性树的 LP 网络来解决这个问题。由于我们是第一个正式化这类 AMM 网络的人，我们谈论的不仅仅是一个新的 DeFi 原语，而是一个将定义 DeFi 下一个时代的新 DeFi 原语类。

2.3 完整树

如果我们扩展上一节讨论的简单树思想，流动性树可以表示为计算图，其中节点表示 LP 操作，弧表示父节点和子节点之间的索引资本转换。由于 DeFi 中使用了各种类型的 LP（例如，恒定加权产品、可组合稳定等），为了便于理解，我们将仅介绍 CPT LP。

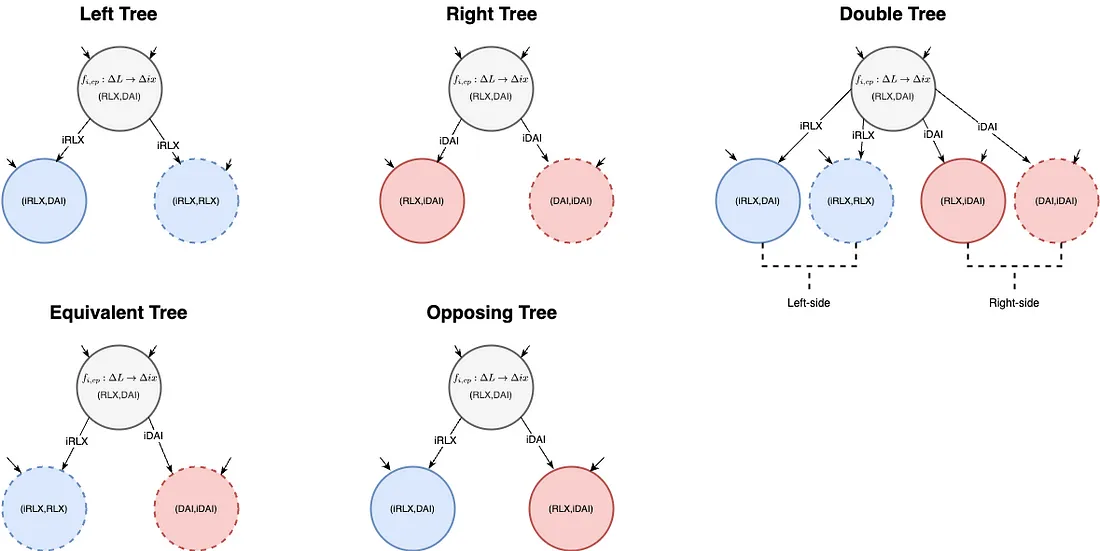
对于资产 x 和 y 的 LP，可以形成的子市场的最大组合为 ix-y、ix-x、ix-iy、x-iy 和 y-iy。完整的流动性树是指利用所有可能的资产组合，在父级下形成最大数量的子 LP；请参阅图 7 以获得直观表示。

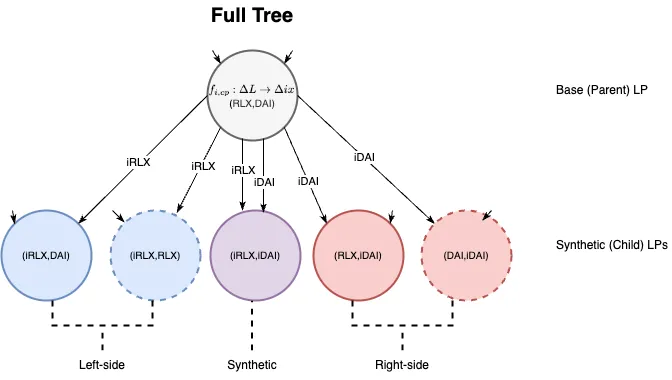
使用其他资产组合，图 7 中的完整树的派生也可以创建成各种子树；参见图 8。模拟向我们展示了这些子树中的每一个都具有略有不同的细微差别，我们将在未来的文章中讨论这些差别。

3、模拟

在本节中，我们使用 2017 年 1 月至 2023 年 11 月的 ETH/USDC 价格数据作为输入来显示模拟输出。我们在 Uniswap V2 左树设置上运行了此程序；参见图 9。

交换、存款和取款金额由从 Gamma 分布中抽取的随机非确定性样本组成，因此没有两次模拟运行会产生相同的输出。为了确保稳健性，我们对模拟进行了 100 次试验，并取结果的中位数，如表 1 所示。

重要的是要注意，可以部署到流动性树子市场的铸造指数代币数量存在上限。例如，如果我们的父池的市值为 100 万美元，那么我们最多可以获得 100 万美元的指数代币。

然而在现实中，树的父 LP 将其 100% 的资本部署到指数代币中的可能性极小，因为一旦资本被铸造，它就不再可用于交易。在这个阶段，我们假设母 LP 将把 10-70% 的资本部署到指数代币中。这就是为什么我们在图 9 中将子 LP 的红色平面描绘得比母 LP 的绿色平面小得多。

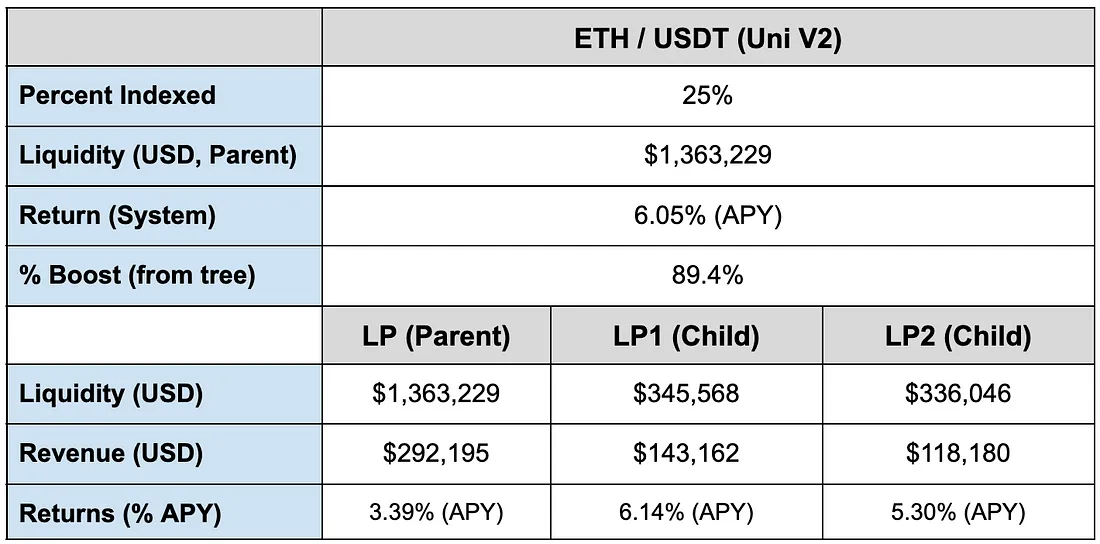
因此，当我们运行这些模拟时，我们保守地假设母 LP 中只有 25% 的资本被部署到子 LP 中，如表 1 第一行所示。

值得讨论的一个有趣特征是，子代的 APY 始终高于父代的 APY。我们发现无论我们运行模拟多少次、使用什么价格样本、交易量或采用什么树配置，情况都是如此。这与子代 LP 中的指数代币价格如何响应父代 LP 中的原生代币价格有关。这是因为子代 LP 中资产价格的波动性比父代 LP 中资产价格的波动性更大。因此，子代资产价格的更高波动性提供了套利机会，而这些机会会被机会主义代理（例如交易机器人）填补。

另一个值得注意的有趣特征是，由于我们看到子 LP 资产价格波动性较大，因此无需将大部分资本铸造为指数代币即可实现显着的绩效提升。表 1 中显示的模拟结果支持了这一点。在这里，我们看到，仅将 25% 的母公司资本部署为指数代币，就可以从子公司获得 89.4% 的绩效提升。更具体地说，我们的结果显示我们从母公司获得 3.39% 的年百分比收益率 (APY)，从整个树中获得全系统 6.05% 的 APY。

4、结束语

本文以序言开始，随后总结了 AMM 的发展历程。我们得出的结论是，到目前为止，所有这些 AMM 都具有的统一特征是它们都是单一 LP 协议。接下来，我们将探讨 AMM 网络的概念，这是一个嵌入合约代码的 AMM 网络。在这一类新的 DeFi 原语中，流动性树可以被认为是最简单的。

我们定义了流动性停滞问题，并通过模拟展示了流动性树如何解决这一问题。流动性树是提高市场效率的好方法，从而获得更高的资本投资回报，如表 1 所示。流动性树让流动性提供者和设计者能够部署更复杂的 DeFi 策略和协议，我们将在接下来的几个月中就即将发布的 Pachira 代币进行讨论。我们相信，这也将在机构层面引发新兴的社会行为，这将成为未来几年 SYS Labs 大量研究的主题。

一旦解决了给定 AMM 的索引问题，就可以将其部署到流动性树中。目前，我们已经解决了 Mooniswap、Uniswap V2 和 V3 协议的索引问题。到目前为止，我们只与 Uniswap V2 公开讨论了这个问题，并将在未来更深入地研究这个问题。我们计划在未来几个月内将 Python 代码发布到流动性树模拟器。与此同时，读者还可以查看 DeFiPy，这是我们的模拟器所依赖的 Python 工具套件。

总之，我们提出了一类新的 DeFi 原语，称为流动性树，它将定义 DeFi 的下一个时代。这是一篇高级介绍性文章，我们计划在未来的文章中更深入地讨论这个主题的技术元素。

原文链接：Liquidity Trees: The Next Epoch of DeFi

DefiPlot翻译整理，转载请标明出处

免责声明：本站资源仅用于学习目的，也不应被视为投资建议，读者在采取任何行动之前应自行研究并对自己的决定承担全部责任。