DEX智能订单路由算法

一键发币： Aptos | X Layer | SUI | SOL | BNB | ETH | BASE | ARB | OP | Polygon | Avalanche | 用AI学区块链开发

本文概述了Deeplink正在进行的研究，即如何将智能订单路由和DEX聚合视为路径查找问题。文章提供了路径查找的简要概述以及一些常用技术，详细解释了这一研究领域如何应用于这些问题，并最后调查了一些相关工作。

1、什么是路径查找？

路径查找是计算领域中确定两点之间最短路线的学科。路径查找算法被广泛应用于许多行业和应用，包括搜索引擎、视频游戏、GPS导航软件和机器人等。

一个简单的例子是GPS路线优化算法，其中节点是地标或目的地，边是这些位置之间的路径，按物理距离加权。通过以最小化总权重的方式遍历这些边，路径查找算法可以找到从一个位置到另一个位置的最短路线。

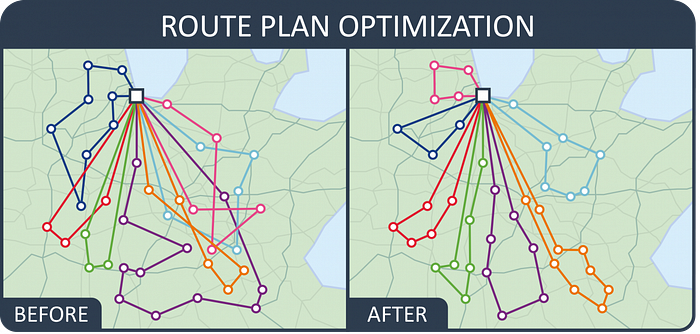
另一个例子类似于Euler的柯尼斯堡七桥问题，可以在基础设施规划如物流、高速公路或铁路设计中找到。例如，在设计复杂的系统如地铁时，重要的是在列车线路布局中最小化冗余旅行，以避免拥堵和缓慢的旅程。一种基本的方法是使用路径查找算法来识别所有相关地铁站之间的最短欧拉路径，也就是说，访问每个车站至少一次的最短路径。一个车站系统也可以分解成离散的线路，每条线路都可以有自己的最短欧拉路径。这可以在Paragon Routing提供的以下表示中看到，Paragon Routing是一家提供路径查找和路线优化软件的公司。

2、术语表

在之前的文章中，我们已经深入探讨了智能订单路由和DEX聚合。为了完全理解路径查找算法在增强这些空间中的必要性，我们建议阅读那些文章。然而，这里也将提供每个概念的简要总结，以及一些重要的初步概念。

智能订单路由

智能订单路由（SOR）是一个自动化过程，旨在通过交易场所找到最理想的路径来处理交易所上的订单。在DEX中，这通常表现为在一组流动性池中找到最佳的交换路径，以利用这些池的流动性深度并减轻碎片化流动性的影响。这种流动性碎片化的首要问题是负面滑点，即在订单放置和执行之间由于现货价格变化而产生的损失。

DEX聚合

DEX是一个由一组流动性池组成的交易平台，它允许资产的交换而无需中央权威或用户放弃对其资产的托管。DEX容易出现上述的流动性碎片化问题，因为它们的资产对被分割成流动性池，随着越来越多的交易场所出现，整体市场流动性变得越来越分散。

DEX聚合器通过聚合和连接多个DEX的服务，使交易者接触到比任何单一DEX所能提供的更多流动性。可以将DEX聚合器类比于Expedia或Google Flights等服务，这些服务将多家航空公司的产品聚合到一个比较服务中，为用户提供最适合其需求的最佳选项。

图

在计算机科学中，路径查找最常使用图——连接节点的集合来表示。在图中，节点可以被视为地点、计算机、人等，具体取决于应用程序，而连接的边可以被视为将这些节点相互关联的东西，例如，代表两个城市节点的边可能代表一条高速公路，或者代表两个资产池的边可能代表这两个池之间的交换。

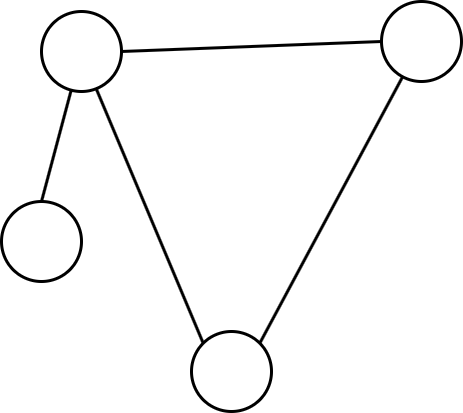
值得注意的是，还有许多其他空间表示方法可用于路径查找，例如网格、二维或三维空间，甚至更抽象的数据结构如八叉树和四叉树。然而，图是最常用的，并且最容易与我们的用例相关联。

加权图

图的边也可以是加权的，赋予节点之间连接的值。例如，在两个城市的例子中，权重可能是城市之间的物理距离，而在资产池的例子中，权重可能表示进行该交换所产生的费用。

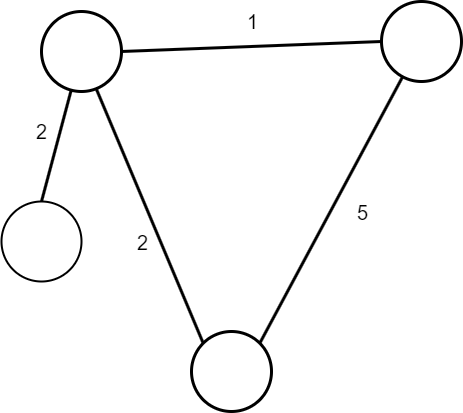
有向图

此外，图可以是有向的，也就是说，某些或所有边只能在一个方向上遍历。也就是说，一个节点可以指向另一个节点，而那个节点不会反过来指向它。例如，如果点A和B之间只有单向道路，那么这就是连接这两个节点的有向边。

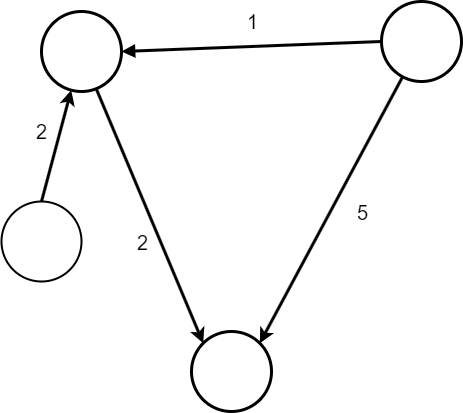
然而，在有向图中，某些节点仍然可以从彼此到达，这通过两个箭头从每个节点指向另一个节点来表示。此外，节点还可以指向自身，表示从该节点到自身的移动是有效的——这被称为循环。

时间图

时间图表示随时间变化的节点和连接。例如，一个节点可能只在临时时间内可用，或者边的权重可能不是随时间恒定的。时间图是图论中相对较新的发展，可以显著增加诸如图遍历等任务的复杂性。时间图是一个新兴领域，性质相当复杂，有关此主题的进一步阅读，这里有一个很好的资源，探索了超出本文范围的深度。

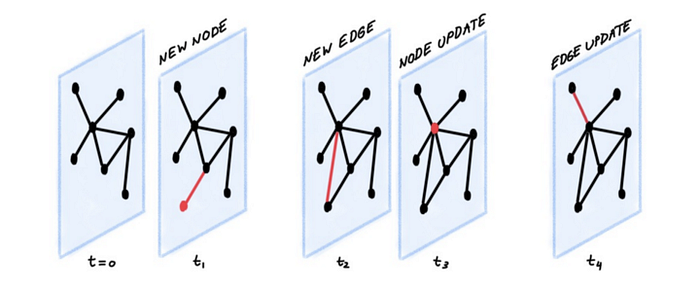
图遍历

当用图表示空间时，路径查找可以表示为图遍历。这通常涉及找到连接两个或多个点的最短路径，通过使用最少的边，或沿连接这些节点的路径累积最少的权重。或者，图遍历可以找到一种路径，以最小化这样做成本的方式访问图中的每个节点。

3、路径查找算法的指标和细节

本节概述了一些术语和概念，有助于理解给定路径查找算法的有效性或适用性。

有信息与无信息算法

有信息算法（如贪心搜索）有一些关于其目标的信息，由用于估计其当前状态与目标状态（在我们的情况下为目标节点）接近程度的函数提供。

相反，无信息算法（如深度优先和广度优先搜索）没有关于其目标的信息。

完整性

如果路径查找算法保证完成执行，即它不会永远运行下去，则认为它是完整的。

终止

路径查找算法可以有一个或多个终止条件，要求其停止执行，例如，如果存在解决方案则找到解决方案。

可接受性

如果在提供足够的时间、内存和计算能力的情况下，路径查找算法能够保证找到最优解，则被认为是可接受的。

大O表示法

大O表示法是描述函数或算法行为的标准数学符号，当相关变量接近特定值（如无穷大）时。它用于表达算法的效率，例如，我们可以这样说，贝尔曼-福特方程需要O(VE)的时间，这意味着我们预计一个具有V个顶点（节点）和E条边的图可以通过贝尔曼-福特算法在V*E步内解决。

4、常见的路径查找算法

路径查找算法大致可以分为三个主要类别：动态、贪心或启发式。本节将概述这些方法之间的差异，并提供每个方法的一些著名示例。

4.1 快速探索随机树

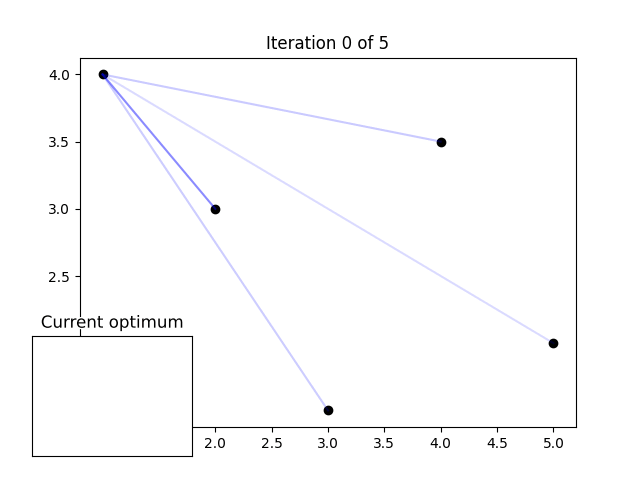
快速探索随机树（RRT）可以根据特定实现的调整方式是贪心或动态的。RRT搜索适用于探索高维空间，特别是用于在非线性系统中找到开环轨迹。因此，当简单的图不能充分表示手头系统的复杂性时，它可能会有用。RRT通过将随机分支扩展到给定空间中最大的未探索区域来实现其遍历；在足够的时间后，它将给出通往所需位置的相对最优路径。它在不知道目标对象的确切位置时也很有用。它是自动驾驶汽车和机器人路径查找和路线优化的行业标准算法，如作者创建的这个演示所示：

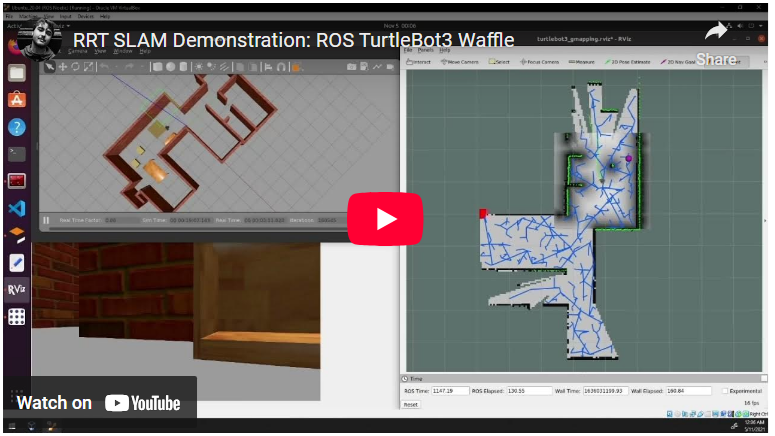
右窗中的蓝色线条描绘了机器人基于RRT的路径查找算法在探索建筑时的分支。

4.2 贪心算法

贪心算法是一种逐步构建解决方案的算法，每一步选择带来最大即时收益的选项，换句话说，就是“贪心”选项。对于贪心算法，无法保证找到最优解，尽管它们通常在内存使用和时间复杂度方面比其对手更高效。

迪杰斯特拉

迪杰斯特拉算法是一种简单但有效的贪心算法，用于在图中找到一个节点到所有其他节点之间的最短路径，或者用于给出任意两个给定节点之间的最短距离。它基本上从给定的源节点开始，依次计算每个节点的距离，每次发现更长的路径时更新最短路径列表。许多其他算法都基于这一概念，但保留了迭代搜索近似最优路径并在发现更好路径时替换它们的原则，直到找到最优路径。

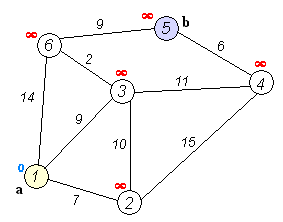
A*

A*通过引入一个启发式函数来优先考虑节点，从而在迪杰斯特拉算法的基础上进行改进，换句话说，它是一个有信息的算法。如果问题适合这样的最优启发式，并且启发式设计得当，启发式可以显著提高A*的性能。与迪杰斯特拉算法类似，A*从源节点开始，然后旨在通过创建和最小化源节点和目标节点之间的路径树，以最小的成本创建到目标的路径，直到达到终止条件——然后选择这些路径中最短的。

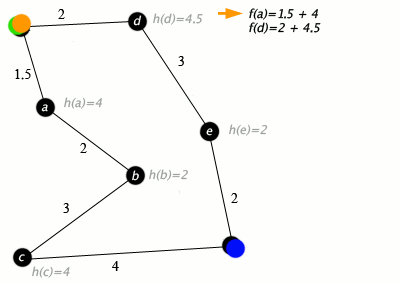
4.3 动态算法

在解决部分问题（子问题）时，动态算法会沿途存储这些子问题的解决方案，然后根据当前情况和之前解决的子问题的解决方案做出决策，以计算最优解决方案。与贪心算法不同，动态算法保证找到最优解（如果存在的话）。然而，作为权衡，它们通常在内存和时间复杂度方面比贪心算法更具挑战性。

贝尔曼-福特

贝尔曼-福特算法基本上与迪杰斯特拉算法和A*具有相同的目的，通常被认为是三种方法中最好的。它可以更慢，但更灵活，因为它可以处理带有混合符号权重（正和负）的图。它通过引入一个松弛方程来实现这一点，该方程本质上通过三角不等式定理使用节点之间的相对距离来计算节点之间的距离，通过与其他已知距离进行比较。

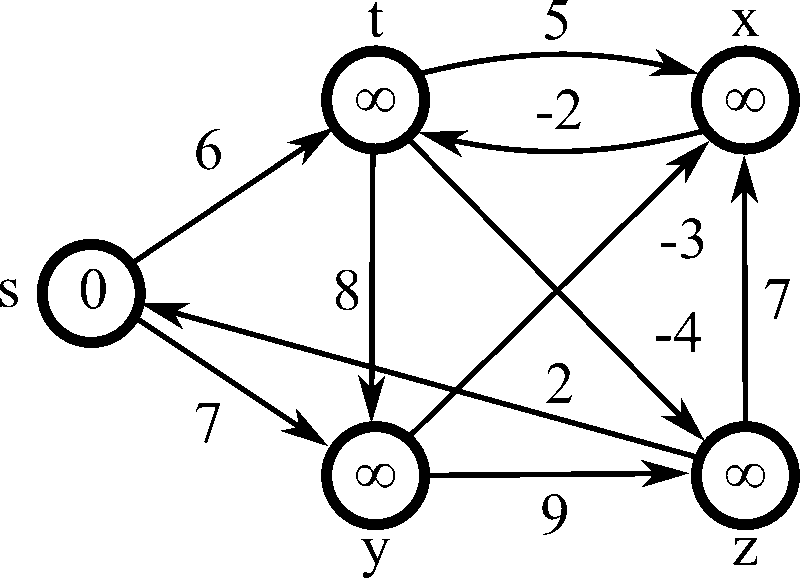
4.4 启发式算法

启发式算法旨在通过牺牲一些最优性和/或完整性，快速有效地解决特定的决策问题。它们最适合用于那些在合理的时间或计算努力范围内无法找到最优解的问题。它们不保证最优性，但可以找到接近最优的或局部最大值/最小值的解决方案，这些解决方案对贪心或动态算法来说仍然是难以解决的。最著名且立即可识别的例子是深度学习模型中的人工神经网络。

蚁群优化

蚁群优化算法旨在通过多代理方法在图中找到路径。人工蚂蚁代理执行局部搜索算法并留下数字信息素供同伴使用，整个人工蚂蚁代理集合留下的累积信息素痕迹通常能找到最优或接近最优的路径，即使在极其庞大或复杂的空间中也是如此。

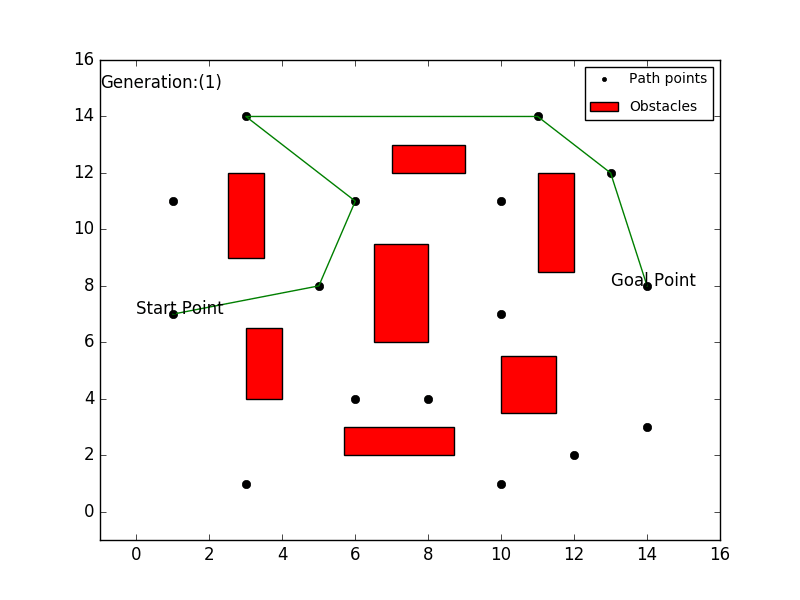
遗传算法

遗传算法基于生物自然选择，这是进化背后的底层过程。生成了一组代理，它们执行对应于其“基因”的一组动作，每个个体都有独特的特征，这些代理有明确的目标和成功指标。代理越成功地实现所需结果，其基因就越有可能被复制到下一代。在路径查找的背景下，这通常涉及代理在给定图中以最低的能量消耗或获取最多资源的方式穿越，将其基因传递给下一代。

5、将智能订单路由表示为DEX聚合的路径查找问题

为了理解为什么在设计DEX聚合器SOR算法时路径查找是一个有用的概念，重要的是记住DEX，以及由此产生的DEX聚合器，本质上是一组流动性池。这些池作为一对资产之间的交换点。以下说明了一个示例，其中DEX被描绘为一个图，在该图上运行路径查找算法以在交易中节省成本。

免责声明：这是一个假设性的、示范性的例子，说明如何将SOR视为路径查找问题

我们可以将这些流动性池的海洋视为一个图，其中池是节点，它们之间的可能交换是边。我们可以继续将其视为一个加权图，其中权重可能代表在两个池之间交换的盈利性或可行性。例如，考虑以下虚构的、相对以DAI为中心的DEX，包含6个流动性池（ETH-WBTC、DAI-WBTC、ETH-DAI、DAI-USDT、DAI-FTM、USDT-FTM）。

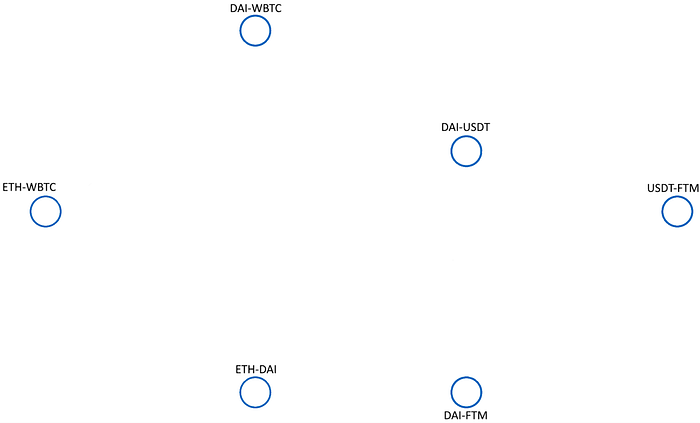
我们立即可以看到存在一个池，可以使我们的交换完成，即ETH-DAI池，但是让我们探讨为什么这可能不是最佳方法。在每个这些节点中，列出的代币之一可以交换为另一个，无论方向。这意味着在交换一个池之后，另一个资产现在被拥有，因此，在与一个池交易后，新资产可以与包含该资产的任何池进行交易。我们将通过创建潜在交换序列的有向图来展示这种关系。

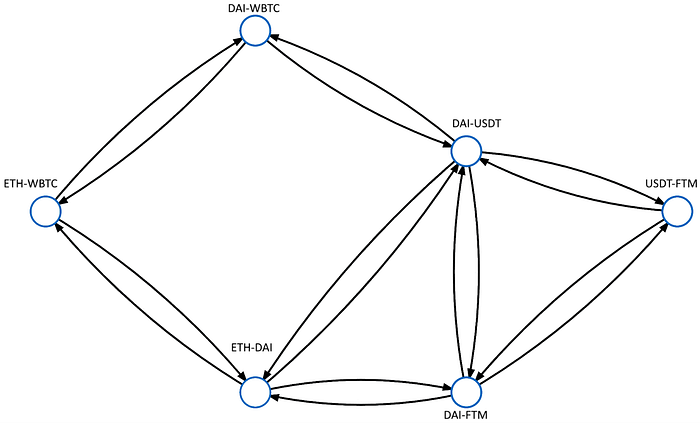
现在，让我们考虑一个场景，其中交易者希望将100 ETH兑换成尽可能多的DAI。我们将任何包含ETH的池标记为绿色源节点，路径从这里开始，任何包含DAI的池标记为橙色目标节点，路径可以在此结束，蓝色节点表示既不是源也不是目标的池。

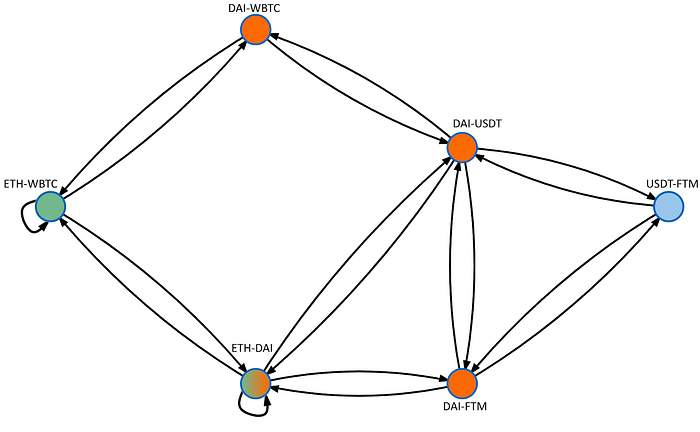
请注意，ETH-DAI池是绿色和橙色的渐变，因为路径可以在此处开始和结束。此外，源节点获得了一个连接到自身的循环，这有助于说明这一点，这也是一个潜在的路径（代表进入图所需的初始交换），以及我们路径查找算法的计算。

接下来，我们为连接节点的边分配权重。我们可以将这视为指向的池中交易的预期滑点百分比，我们可以假设这是通过各种因素计算的，包括流动性集中度、流动性范围、波动性等——您可以在我们的关于智能订单路由的文章中了解更多有关滑点原因的信息。这些边可能需要机器学习技术来计算，我们在关于DEX聚合和SOR的机器学习技术的文章中探讨了这些技术，但为了本解释的目的，这些数字是随意选择的。

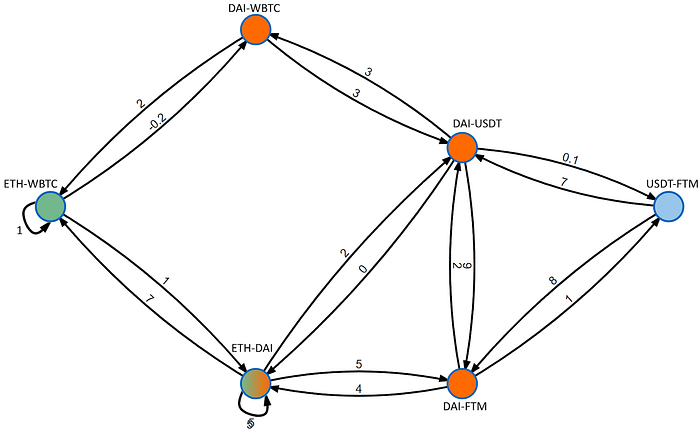
请注意，WBTC与DAI的交换被分配了一个负权重，表示通过套利可能获得0.2%的利润。还值得一提的是，像迪杰斯特拉这样的算法无法处理这种情况，因为它们无法遍历多符号图。

我们可以看到，最简单的交易是直接使用一个池，将ETH兑换为DAI，导致5%的滑点损失（5 ETH，或截至本文写作时的10,274.31美元）。然而，让我们检查我们的另一个源节点，ETH-WBTC池，通过确定它与所有其他池之间的最短路径。任何之前讨论过的路径查找算法都可以处理这个任务，但在本演示中，我们将任意地通过在图上运行贝尔曼-福特算法，从ETH-WBTC池开始来完成。

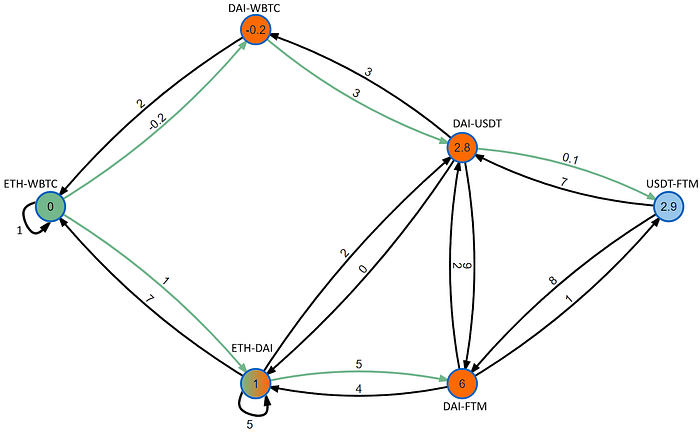
绿色边表示从ETH-WBTC节点到图中所有其他节点的路线。节点中的数字表示到达这些节点的成本（滑点的累计百分比损失）。在这里，我们可以看到，通过利用在WBTC与DAI交易中的套利机会，我们可以减少一些滑点损失。假设我们的算法选择70-30的拆分，首先在ETH-WBTC中交易70 ETH，然后将该WBTC兑换为DAI，然后在ETH-DAI池中直接交易70 ETH。

0.3*0.5 + 0.7(0.1–0.02) = 0.206%

这表明与仅使用一个池的简单方法相比，节省了4.79%，约合9,857.24美元。请记住，这些值是随意选择的，真实的DEX可能会因滑点损失更大（参见我们的DEX聚合器文章中的真实示例）。

此外，这种方法只是说明了如何将SOR视为路径查找问题，更复杂的路径查找方法可能需要，而且可能会产生更令人印象深刻的结果。需要采用更复杂的路径查找技术的一个原因是大型DEX聚合器相关的图的规模。我们的例子使用了一个只有7个流动性池的假设DEX，而真实的DEX和DEX聚合器可能正在处理数千个节点，这可能导致边的数量呈指数级增长。在所需时间尺度内以完美最优性遍历这样的图是不可行的。因此，可能需要专门用于接近最优性的算法（如ACO或遗传算法）以跟上复杂性要求。

此外，构建图及其边的任务可能比一旦创建图后遍历图更为复杂。选择有效的池，决定是否拆分订单以及拆分的大小和数量，分配权重

原文链接：Pathfinding Algorithms for DEX Aggregation and Smart Order Routing

DefiPlot翻译整理，转载请标明出处

免责声明：本站资源仅用于学习目的，也不应被视为投资建议，读者在采取任何行动之前应自行研究并对自己的决定承担全部责任。