tech

用Python构建通胀对冲策略

本文的范围是实际考察CPi和黄金的相关性，并找到一种投资策略，将这种知识转化为优势，给我们带来什么？利润。

一键发币： Aptos | X Layer | SUI | SOL | BNB | ETH | BASE | ARB | OP | Polygon | Avalanche | 用AI学区块链开发

消费者价格指数（CPI）是一个用于衡量商品和服务平均价格上涨的指标，这会影响我们的日常开支。是的！即使是交易者也应该吃饭和睡觉（好吧，第二个可能不太确定…）。我们通常的支出增加通常会压低股票，比如股份。因此，我们从两边都被打败了吗？不。

黄金是应对这一挑战的平衡器，在历史上，当通货膨胀增加时，投资者会找到他们的份额，投资于黄金，黄金的价格与股票相反移动。确切的“为什么”完全是理论性的，并且有些有争议，因为黄金只是金属，其价格基于人们愿意为其支付的价格，没有其他用途。但这不在我们文章的范围内进行探讨……

本文的范围是实际考察这种相关性，并找到一种投资策略，将这种知识转化为优势，给我们带来什么？利润。

通过使用Python和FinancialModelingPrep的API套件，我们将：

获取CPI和黄金的价格
计算并讨论这两个之间的相关性
设计一个策略，在高通胀期间投资黄金，而在其他情况下投资标普500，并
讨论回测的结果

1、让我们开始编码

首先，我们将定义本文中将使用的包。我们将设置一个从1975年开始的50年周期。

import requests  
import matplotlib.pyplot as plt  
import pandas as pd  

token = 'YOUR FMP API KEY'  
fromdate = '1975-01-01'  
todate = '2025-10-02'

第一步是使用FMP的经济指标API获取经济指标，特别是CPI。

url = f'https://financialmodelingprep.com/stable/economic-indicators'  
name = 'CPI'  
querystring = {"apikey":token, "name":name, "from":fromdate, "to":todate}  

resp = requests.get(url, querystring).json()  

df_cpi = pd.DataFrame(resp)  
df_cpi.drop(columns=["name"], inplace=True)  
df_cpi.tail(5)

如您所见，我们收到的数据是每月的。CPI不是每天计算的指数；它由美国劳工统计局（BLS）每月发布，这在本文的范围内。

现在，我们将使用FMP的轻量级图表API，该API提供资产和其他资产（如黄金）的历史EOD价格。

url = f'https://financialmodelingprep.com/stable/historical-price-eod/light'  
symbol = 'GCUSD'  

querystring = {"apikey":token, "symbol":symbol, "from":fromdate, "to":todate}  
resp = requests.get(url, querystring).json()  

df_gold = pd.DataFrame(resp)  
df_gold.drop(columns=["symbol","volume"], inplace=True)  
df_gold.tail(5)

如您所见，对于黄金，我们有每日价格，所以首先要做的就是合并这两个数据框，但只保留每月初的黄金价格。这有点棘手，因为当月初（我们有CPI价格）是周末时，我们将没有黄金价格。我们将使用merge_asof和direction='backward'来解决这个问题。

df_cpi['date'] = pd.to_datetime(df_cpi['date']).dt.normalize()  
df_gold['date'] = pd.to_datetime(df_gold['date']).dt.normalize()  

df_cpi_sorted = df_cpi.sort_values('date')  
df_gold_sorted = df_gold.sort_values('date')  

df_cpi_gold = pd.merge_asof(  
    df_cpi_sorted,  
    df_gold_sorted,  
    on='date',  
    direction='backward'  
).reset_index(drop=True)  

df_cpi_gold = df_cpi_gold.rename(columns={'value': 'cpi', 'price': 'gold'})  
df_cpi_gold.tail(5)

如您所见，我们现在有了一个完美的月度数据框，其中CPI和黄金的价格已经对齐。

现在，让我们计算这50年间的相关性。

subset = df_cpi_gold[['cpi', 'gold']].dropna()  
value_price_corr = subset['cpi'].corr(subset['gold'], method='pearson')  
pd.DataFrame({'cpi_gold_pearson_correlation': [value_price_corr]})

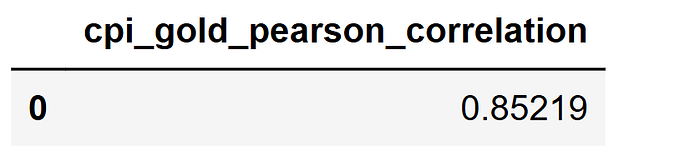
相关性为0.85。这是一个非常高的数字，表明历史上CPI和黄金往往朝同一方向移动。当CPI上升时，黄金也上升，反之亦然。

但我们不需要等待50年才能证明这一点。事实上，这是不正确的，因为情况可能已经改变，或者可能存在一段时间方向相反。我们将使用滚动相关性来研究这一点。我们将周期减少到10年，看看结果。

years = 10  
window = years*12  
df_cpi_gold['rolling_corr'] = df_cpi_gold['cpi'].rolling(window=window, min_periods=window).corr(df_cpi_gold['gold'])  

plt.figure(figsize=(12, 4))  
plot_data = df_cpi_gold[['date', 'rolling_corr']].dropna()  
plt.plot(plot_data['date'], plot_data['rolling_corr'])  
plt.title(f'Rolling {years}-Years Correlation: CPI Value vs Gold Price')  
plt.xlabel('Date')  
plt.ylabel('Correlation')  
plt.ylim(-1, 1)  
plt.grid(True, alpha=0.3)  
plt.tight_layout()  
plt.show()

输出：

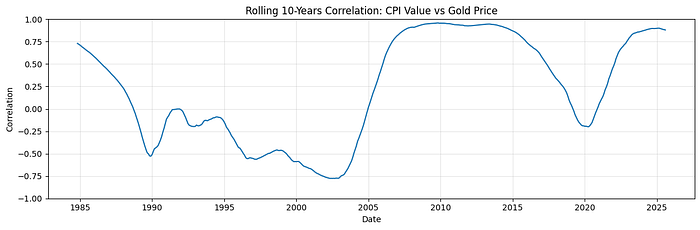
这张图非常有趣。看起来在90年代和2000年代初以及2020年，相关性是不存在的，有时甚至转为负数，这意味着CPI和黄金朝相反方向移动。可能的解释如下：

在90年代和2000年代初，我们经历了各种可以解释这种情况的事件。我们有严格的货币政策，导致CPI较低，以及通胀挂钩债券的引入为机构投资者提供了黄金以外的替代品。
然后是新冠疫情的到来……显然，在黑天鹅事件中，没有什么可做的。当时无法预测CPI，而黄金主要受到全球恐惧和流动性注入的驱动。

在90年代和2020年观察到的例外情况，而不是挑战相关性的前提，实际上测试了它，从而证明了CPI和黄金之间总体关系的存在，显示了在典型经济条件下相关性存在。

2、让我们进行回测

但是，利用这些信息是否能获得优势？能否确定何时投资股票，何时投资黄金？

因此，我们将回测一个简单的理论。当CPI处于前一个月变化的前20%时，我们将投资黄金。在所有其他情况下，我们将投资标普500。

首先，我们需要将标普500的价格加入我们的数据框。这将通过以下Python代码完成，并将其合并到初始数据框中，像之前一样，复制到名为df_backtest的新数据框中。

ticker = '^GSPC'  
url = f'https://financialmodelingprep.com/api/v3/historical-price-full/{ticker}'  
querystring = {"apikey":token, "from":fromdate, "to":todate}  
data = requests.get(url, querystring)  

if data.status_code != 200:  
    print(f"Error: {data.status_code}")  
    print(data.text)  
data = data.json()  

df_sp500 = pd.DataFrame(data['historical'])  

df_cpi_gold['date'] = pd.to_datetime(df_cpi_gold['date']).dt.normalize()  

sp = df_sp500[['date', 'adjClose']].copy()  
sp['date'] = pd.to_datetime(sp['date']).dt.normalize()  
sp = sp.sort_values('date').rename(columns={'adjClose': 'sp500'})  

df_backtest = pd.merge_asof(  
    df_cpi_gold.sort_values('date'),  
    sp,  
    on='date',  
    direction='backward'  
).reset_index(drop=True)  

df_backtest = df_backtest[['date', 'cpi', 'gold', 'sp500']]  
df_backtest.tail(5)

为了测试我们的策略，我们还需要计算CPI、黄金和标普500的百分比变化。

df_backtest['cpi_pct_change'] = df_cpi_gold['cpi'].pct_change()  
df_backtest['gold_pct_change'] = df_cpi_gold['gold'].pct_change()  
df_backtest['sp500_pct_change'] = df_backtest['sp500'].pct_change()  
df_backtest

此外，我们还需要做以下事情：

计算CPI的80%阈值，以了解通货膨胀是否高于它。
我们将计算一个信号列，如果为真，则表示我们高于80%，所以我们处于通货膨胀时期。
最后，根据这个月的信号，分别使用黄金或标普500的回报率

注意：我们将信号移位3个周期。原因是即使我们有第一个月的通货膨胀信息，这个信息也要等到月中之后才会公布。因此，我们将略微惩罚我们的策略，使用1或2周后的信息，具体取决于CPI的发布时间。

df_backtest.dropna(inplace=True)  
df_backtest['quantile_threshold'] = df_backtest['cpi_pct_change'].rolling(window=1000, min_periods=1).quantile(0.8)  
df_backtest['signal'] = (df_backtest['cpi_pct_change'] > df_backtest['quantile_threshold']).shift(3)  

df_backtest['strategy_return'] = df_backtest['gold_pct_change'].where(df_backtest['signal'],  
                                                                      df_backtest['sp500_pct_change'])  
df_backtest

最后，基于每个月的百分比变化，我们将计算权益，就好像我们在1975年投资了1美元，并确定今天我们的回报是多少。

df_backtest['gold_equity'] = (1 + df_backtest['gold_pct_change']).cumprod()  
df_backtest['sp500_equity'] = (1 + df_backtest['sp500_pct_change']).cumprod()  
df_backtest['strategy_equity'] = (1 + df_backtest['strategy_return']).cumprod()  

df_backtest[["gold_equity", "sp500_equity", "strategy_equity"]].tail(1)

这非常有希望。在我们的场景中，如果你投资了1美元的黄金50年，你现在将拥有19.1美元，如果你投资了标普500，你将拥有81美元。通过我们正在回测的策略，你将拥有141.1美元！这是一个非凡的结果。

让我们绘制它！

required_cols = {'date', 'gold_equity', 'sp500_equity', 'strategy_equity'}  
missing = required_cols - set(df_backtest.columns)  
if missing:  
    raise ValueError(f"Missing required columns in df_backtest: {missing}")  

df_plot_eq = df_backtest.copy()  
df_plot_eq['date'] = pd.to_datetime(df_plot_eq['date'])  
df_plot_eq = df_plot_eq.sort_values('date')  

plt.figure(figsize=(11, 6))  
plt.plot(df_plot_eq['date'], df_plot_eq['gold_equity'], label='Gold Equity', linewidth=1.5)  
plt.plot(df_plot_eq['date'], df_plot_eq['sp500_equity'], label='S&P 500 Equity', linewidth=1.5)  
plt.plot(df_plot_eq['date'], df_plot_eq['strategy_equity'], label='Strategy Equity', linewidth=2.0)  

plt.title('Equity Curves: Gold vs S&P 500 vs Strategy')  
plt.xlabel('Date')  
plt.ylabel('Equity (Cumulative, base=1.0)')  
plt.grid(True, alpha=0.3)  
plt.legend()  
plt.tight_layout()  
plt.show()

输出：

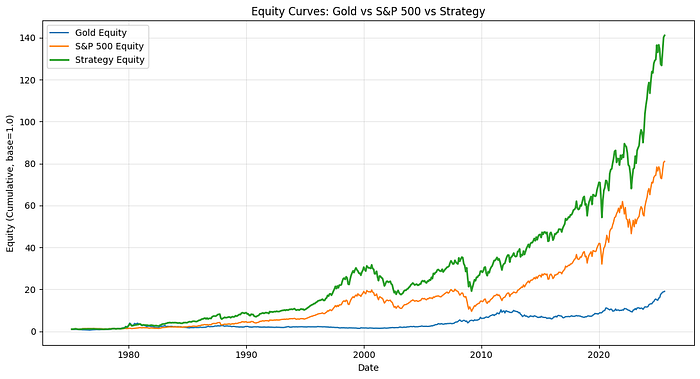
这张图非常有说服力。图表主要像标普500一样移动，在我们投资黄金时推动更高。

让我们看看一些风险指标，首先是最大回撤。

def calculate_max_drawdown(returns):  
    wealth_index = (1 + returns).cumprod()  
    running_max = wealth_index.cummax()  
    drawdown = (wealth_index - running_max) / running_max  
    max_drawdown = drawdown.min()  
    return max_drawdown  

print(f'GOLD has maximum drawdown of {calculate_max_drawdown(df_backtest["gold_pct_change"])}')  
print(f'SP500 has maximum drawdown of {calculate_max_drawdown(df_backtest["sp500_pct_change"])}')  
print(f'Strategy has maximum drawdown of {calculate_max_drawdown(df_backtest["strategy_return"])}')

显然，在50年的时间里，最大回撤并不是任何投资者的梦想。然而，我们应该从结果中记住的是，我们的策略的回撤小于黄金或标普500在此期间经历的回撤。

现在让我们尝试夏普比率。

def calculate_sharpe_ratio(returns, risk_free_rate, periods_per_year):  
    excess_return = returns - risk_free_rate / periods_per_year  
    mean_excess_return = excess_return.mean() * periods_per_year  
    vol = excess_return.std() * (periods_per_year ** 0.5)  
    sharpe_ratio = mean_excess_return / vol  
    return sharpe_ratio  

print(f'GOLD has Sharpe Ratio of {calculate_sharpe_ratio(df_backtest["gold_pct_change"], risk_free_rate=0.02, periods_per_year=12)}')  
print(f'SP500 has Sharpe Ratio of {calculate_sharpe_ratio(df_backtest["sp500_pct_change"], risk_free_rate=0.02, periods_per_year=12)}')  
print(f'Strategy has Sharpe Ratio of {calculate_sharpe_ratio(df_backtest["strategy_return"], risk_free_rate=0.02, periods_per_year=12)}')

即使在夏普比率方面，评论也可以是相同的。该策略实际上具有与标普500相似（略好）的夏普比率，证明了通过这种策略，我们不会为了回报而增加风险。

3、这并不正确

结果非常有希望，因此讨论这种方法的潜在缺陷是有意义的。然而，我们首先应该承认，尽管回测方法值得怀疑，但我们不应完全忽视结果，并应继续我们的调查。显然，在一篇简单的博客文章中，这并不总是可行的，您需要仔细考虑下一步行动，以实现您的盈利目标。不过，这种方法的潜在缺点包括以下几点：

拥有50年的数据并不一定意味着比10年或20年更好。投资环境随着时间的推移而变化。例如，在70年代投资黄金或标普500可能不同（也许甚至用那些老式手机？），而今天你可以从你的手机上进行投资。
20%的信号在整个时期内过于简单，可以被视为过度简化或过拟合。
我们忽略了其他资产类别，如债券，它们是另一种对冲通胀飙升和衰退的安全避风港。
尽管该策略的回撤比其他策略更好，但47%的回撤仍然不是您应在投资策略中追求的目标。
回测中没有考虑任何费用、滑点或其他可能显著改变结果的因素。